المثلثات هي أشكال هندسية تتكون من زوايا وأضلاع قد تكون متساوية أو مختلفة، لكن هناك شيء واحد ثابت في كل المثلثات، وهو أن كل مثلث يتكون من ثلاث أضلاع وثلاث زوايا داخلية.
فيما يلي بعض الأمثلة على أنواع من المثلثات:
- المثلث قائم الزاوية فيه زاوية واحدة بقياس 90 درجة وزاويتان حادتان.
- المثلث المتساوي الساقين فيه زاويتان متساويتان في القياس وضلعان متساويان في الطول.
- المثلث متساوي الأضلاع تكون جميع زواياه متساوية القياس وجميع أضلاعه متساوية الطول.
- المثلث مختلف الأضلاع تكون زواياه مختلفة القياسات وأضلاعه مختلفة الأطوال.
على الرغم من وجود العديد من أنواع المثلثات بحسب قياسات الزوايا أو أطوال الأضلاع، إلا أن جميعها تتبع نفس القواعد والخصائص.
ستتعرف في هذه المقالة على الزوايا الداخلية للمثلث ونظرية مجموع زوايا المثلث، وكيف تستخدم هذه النظرية لمعرفة قياسات الزوايا الداخلية للمثلث؟
ما هي الزاوية الداخلية للمثلث؟
في الهندسة، الزوايا الداخلية للمثلث هي الزوايا التي تتكون داخل المثلث.
الزوايا الداخلية لها الخصائص التالية:
- مجموع قياسات الزوايا الداخلية هو 180 درجة (نظرية مجموع زوايا المثلث).
- كل زاوية من الزوايا الداخلية للمثلث قياسها أكبر من 0 درجة وأصغر من 180 درجة.
- تتقاطع منصفات الزوايا الداخلية الثلاث داخل المثلث عند نقطة هي مركز الدائرة الملامسة لأضلاع المثلث من الداخل.
- مجموع قياس كل زاوية داخلية مع الزاوية الخارجية المجاورة يساوي 180 درجة (خط مستقيم).
ما هي نظرية مجموع زاوية المثلث؟
إحدى الخصائص المعروفة حول كل المثلثات هي أن مجموع زواياها الداخلية الثلاث يساوي 180 درجة.
نص لنظرية مجموع زاوية المثلث هي: “مجموع قياسات الزوايا الداخلية الثلاث في المثلث هو دائمًا 180 درجة”.
يمكننا من هذه النظرية أن نستنتج أن:
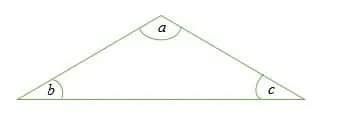
a + b + c = 180
كيف تجد الزوايا الداخلية للمثلث؟
عندما تُعرف قياس زاويتان داخليتان للمثلث، فمن الممكن تحديد قياس الزاوية الثالثة باستخدام نظرية مجموع زاوية المثلث. لإيجاد الزاوية الثالثة غير المعروفة لمثلث، اطرح مجموع الزاويتين المعروفتين من 180.
دعنا نلقي نظرة على بعض الأمثلة على استخدامات هذه النظرية:
مثال 1
في المثلث ABC، قياس الزاوية A = 38 درجة، وقياس الزاوية B = 134. احسب قياس الزاوية C.
الحل
تنص نظرية مجموع زوايا المثلث على: “مجموع قياسات الزوايا الداخلية الثلاث في المثلث هو دائمًا 180 درجة”.
إذًا فإن:
A + B + C = 180
38 + 134 + C = 180
C = 38 + 134 – 180
C = 8
مثال 2
أوجد قياس الزاويتين x في المثلث الموضح أدناه.
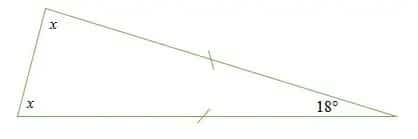
الحل
المثلث في هذا المثال متساوي الساقين لأن فيه ضلعين متساويين في الطول.
في المثلث المتساوي الساقين، تكون زاويتا القاعدة متساويتان في القياس. هذا يعني أن الزاوية x الأولى تساوي الزاوية x الثانية.
حسب نظرية مجموع زاوية المثلث، مجموع الزوايا الداخلية للمثلث = 180 درجة.
هذا يعني أن:
x + x + 18 = 180
2x + 18 = 180
2x = 180 – 18
2x = 162
x = 162 ÷ 2
x = 81
مثال 3
أوجد قياس الزوايا x في المثلث أدناه.
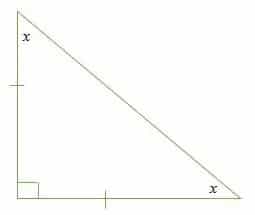
الحل
هذا المثلث قائم الزاوية ومتساوي الساقين: هذا يعني أن قياس زاوية واحدة منه هي 90 درجة.
في المثلث المتساوي الساقين، تكون زاويتا القاعدة متساويتان في القياس. هذا يعني أن الزاوية x الأولى تساوي الزاوية x الثانية.
حسب نظرية مجموع زاوية المثلث، مجموع الزوايا الداخلية للمثلث = 180 درجة.
هذا يعني أن:
x + x + 9 = 180
2x + 90 = 180
2x = 180 – 90
2x = 90
x = 90 ÷ 2
x = 45
مثال 4
أوجد قياس زوايا مثلث قياس زاويته الثانية أكبر من قياس الزاوية الأولى بمقدار 15 درجة، وقياس الزاوية الثالثة يزيد بمقدار 66 درجة عن الزاوية الثانية.
الحل
لنفرض أن الزاوية الأولى a
ونفرض الزاوية الثانية b، فتكون b = a + 15
نفرض الزاوية الثالثة c، فتكون c = a + 15 + 66
حسب نظرية مجموع زاوية المثلث، مجموع الزوايا الداخلية للمثلث = 180 درجة.
هذا يعني أن:
a + b + c = 180
a + (a + 15) + (a + 15 + 66) = 180
3a + 96 = 180
3a = 180 – 96
3a = 84
a = 28
ولأن b = a + 15
b = 28 + 15 = 43
ولأن c = b + 66
c = 43 + 66 = 109
إذًا زوايا المثلث هي 28 + 43 + 109 = 180
مثال 5
أوجد الزوايا الداخلية المجهولة في الشكل التالي.
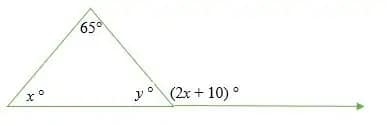
الحل
الزاوية y و (2x + 10) زاويتان مكملتان (مجموعهما = 180 درجة)
هذا يعني أن:
y + 2x + 10 = 180
y + 2x = 180 – 10
y + 2x = 170
y = 170 – 2x ………… I
من نظرية مجموع زاوية المثلث:
x + y + 65 = 180
x + y = 180 – 65
x + y = 115 …………..II
نعوض y في المعادلة I بالمعادلة II:
x + 170 – 2x = 115
-x = 115 – 170
-x = – 55
x = 55
بعد أن أوجدنا قيمة x، نستطيع إيجاد قيمة y كم خلال نظرية مجموع زوايا المثلث:
x + y + 65 = 180
55 + y + 65 = 180
y = 180 – 120
y = 60
إذًا فإن قياسات الزوايا المجهولة هي x = 55 وy = 60 .
مثال 6
احسب قياس الزاوية x لمثلث زواياه: x و (x + 20) و (2x + 40)
الحل
مجموع الزوايا الداخلية = 180 درجة
x + (x + 20) + (2x + 40) = 180
نبسط المعادلة:
x + x + 2x + 20 + 40 = 180
4x + 60 = 180
4x = 180 – 60
4x = 120
x = 120 ÷ 4
x = 30
هذا يعني أن قياس الزاوية الثانية هو 20 + 30 = 50 درجة
قياس الزاوية الثالثة هو 40 + (30 × 2) = 100 درجة
مثال 7
أوجد الزوايا المجهولة في الشكل أدناه.
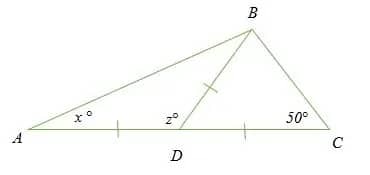
الحل
المثلث ADB هو مثلث متساوي الساقين لأن طول AD = BD.
المثلث BDC هو مثلث متساوي الساقين لأن طول BD = CD.
نوجد زوايا المثلث BDC:
في المثلث BDC، زاويتا القاعدة متساوية، هذا يعني أن الزاويين C = B = 50
ولأن مجموع زوايا المثلث 180 درجة، يكون:
B + C + D = 180
50 + D = 180
D = 180 – 50
D = 130
الزاويان D و z متكاملتان. هذا يعني أن:
D + z = 180
130 + z = 180
z = 180 – 130
z = 50
في المثلث ADB، الزاوية B = x لأن المثلث متساوي الساقين.
مجموع الزوايا الداخلية z + x + B = 180 درجة
50 + x + B = 180
لأن B = x يصبح لدينا:
50 + x + x = 180
2x = 180 – 50
2x = 130
x = 65
B = x = 65
المصدر